-
題目不完整,無法得出具體問題及答案。請(qǐng)補(bǔ)充完整問題內(nèi)容。
-
在平行四邊形abcd中,ab=20,ad=30,角2113abc=60,點(diǎn)5261q從b出發(fā)沿4102ba向a移動(dòng),速度為2cm/s,點(diǎn)P從點(diǎn)D出發(fā)沿DC向點(diǎn)C勻速運(yùn)動(dòng),速度為3cm/s,當(dāng)P停止運(yùn)1653動(dòng)時(shí),點(diǎn)Q也隨之停止運(yùn)動(dòng),過點(diǎn)P做PM⊥AD交AD于點(diǎn)M,連接PQ、QM,設(shè)運(yùn)動(dòng)的時(shí)間為t s(0<t≤6)
(1)當(dāng)PQ⊥PM時(shí),求t的值
(2)設(shè)△PQM的面積為y(cm?),求y于t之間的函數(shù)關(guān)系式
(3)是否存在某一時(shí)刻使得△PQM的面積最大?若存在,求出此時(shí)t的值,并求出最大面積,若不存在,請(qǐng)說明理由
(4)過點(diǎn)M作MN//AB交BC于點(diǎn)N,連接點(diǎn)N
,是否存在某一時(shí)刻使得PM=PN,求出此時(shí)t的值,若不存在,請(qǐng)說明理由
解:(1)當(dāng)PQ//AD,因?yàn)锳Q//PD,
所以四邊形AQPD是平行四邊形,
所以AQ=PD,
所以20-2t=3t,
解得,t=4,
即當(dāng)t=4時(shí),PQ//AD。
(2)因?yàn)锽Q=2t,PD=3t,所以AQ=20-2t,
因?yàn)椤螦BC=60°,所以∠D=60°
因?yàn)镻M⊥AD,所以∠PMD=30°,
所以MD=1/2PD=3/2t,MP=3√3/2t
過Q點(diǎn)作QE⊥AD交DA的延長(zhǎng)線于點(diǎn)E,過C點(diǎn)作CD⊥AB交AB于點(diǎn)D,
因?yàn)椤螦BC=60°,所以∠QAE=60°,
所以QE=AQ/sin60°=√3/3(40-4t),CF=BC/sin60°=15√3,
因?yàn)镾△PQM=S梯形AQOD-S△AQM-S△PMD,
即y=1/2×(AQ+PD)×CF-1/2×AM×QE-1/2×MD×MP=1/2×(20-2x+3x)×15√3-1/2×(30-3/2x)×√3/3(40-4t)-1/2×3/2t×3√3/2t
化簡(jiǎn)得,y=-15√3t?/8+105√3t/4
因?yàn)?t≤20,3t≤20,所以t≤20/3。
所以y與t的函數(shù)關(guān)系式為y=-15√3t?/8+105√3t/4(0<t≤20/3)。 -
原題如下:
在平2113行四邊形abcd中,5261ab=20,ad=30,角abc=60,點(diǎn)4102q從b出發(fā)沿1653ba向a移動(dòng),速度為2cm/s,點(diǎn)P從點(diǎn)D出發(fā)沿DC向點(diǎn)C勻速運(yùn)動(dòng),速度為3cm/s,當(dāng)P停止運(yùn)動(dòng)時(shí),點(diǎn)Q也隨之停止運(yùn)動(dòng),過點(diǎn)P做PM⊥AD交AD于點(diǎn)M,連接PQ、QM,設(shè)運(yùn)動(dòng)的時(shí)間為t s(0<t≤6)
(1)當(dāng)PQ⊥PM時(shí),求t的值
(2)設(shè)△PQM的面積為y(cm²),求y于t之間的函數(shù)關(guān)系式
(3)是否存在某一時(shí)刻使得△PQM的面積最大?若存在,求出此時(shí)t的值,并求出最大面積,若不存在,請(qǐng)說明理由
(4)過點(diǎn)M作MN//AB交BC于點(diǎn)N,連接點(diǎn)N,是否存在某一時(shí)刻使得PM=PN,求出此時(shí)t的值,若不存在,請(qǐng)說明理由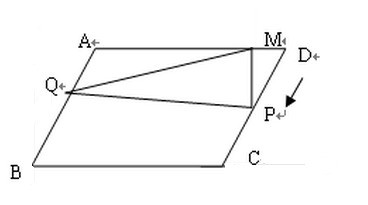
解:(1)當(dāng)PQ//AD,因?yàn)锳Q//PD,
所以四邊形AQPD是平行四邊形,
所以AQ=PD,
所以20-2t=3t,
解得,t=4,
即當(dāng)t=4時(shí),PQ//AD。
(2)因?yàn)锽Q=2t,PD=3t,所以AQ=20-2t,
因?yàn)椤螦BC=60°,所以∠D=60°
因?yàn)镻M⊥AD,所以∠PMD=30°,
所以MD=1/2PD=3/2t,MP=3√3/2t
過Q點(diǎn)作QE⊥AD交DA的延長(zhǎng)線于點(diǎn)E,過C點(diǎn)作CD⊥AB交AB于點(diǎn)D,
因?yàn)椤螦BC=60°,所以∠QAE=60°,
所以QE=AQ/sin60°=√3/3(40-4t),CF=BC/sin60°=15√3,
因?yàn)镾△PQM=S梯形AQOD-S△AQM-S△PMD,
即y=1/2×(AQ+PD)×CF-1/2×AM×QE-1/2×MD×MP=1/2×(20-2x+3x)×15√3-1/2×(30-3/2x)×√3/3(40-4t)-1/2×3/2t×3√3/2t
化簡(jiǎn)得,y=-15√3t²/8+105√3t/4
因?yàn)?t≤20,3t≤20,所以t≤20/3。
所以y與t的函數(shù)關(guān)系式為y=-15√3t²/8+105√3t/4(0<t≤20/3)。
(3)S△MPQ關(guān)于時(shí)間t的關(guān)系式是:S△MPQ=0.5×2×sin60°t×(30×sin60°-5×cos60°t)=22.5t-t²√3/4【0≤t≤20/3】,在0≤t≤20/3內(nèi)單邊遞增,所以S△MPQ最大值為150-100√3/4【t=20/3】
(4)MP=3tsin60°=1.5t√3,NP=√[100+(10√3-1.5t√3)²],
MP=NP,6.75t²=100+3(10-1.5t)²,t=40/9≤20/3,所以t=40/9符合題意存在該時(shí)刻滿足MP=NP。 -
首先:PB= 1×t = t , CQ = 1×t= t , BQ = 12- t .
過P作PH⊥BC,H為垂足。
∵∠B=30°,PH⊥BC
∴ PH= PB的一半即 t / 2 。
∴ S△PBQ = (12-t )×t/2 ÷2 = - 3/4t? + 3t 。是二次函數(shù)。
注意:還有一種情況: P到了AD上(t >4時(shí))。
此時(shí) △PBQ 的高就是梯形的高2.( 梯形的高你另外算:過A畫高h(yuǎn),則h=AB的一半)
那么,此時(shí) S△PBQ =(12-t )×2 ÷2 = 12-t 。 是一次函數(shù)。
(2)在整個(gè)運(yùn)動(dòng)過程中,存在某一時(shí)刻t,A、B、Q、P四點(diǎn)恰好構(gòu)成一個(gè)平行四邊形!
A、B、Q、P四點(diǎn)恰好構(gòu)成一個(gè)平行四邊形,則有:AP=BQ .
則 t-4 = 12-t
則 t=8
.( 梯形的高你另外算:過A畫高h(yuǎn),∵∠B=30°,當(dāng)然 h=AB的一半=4的一半=2)
-
解:設(shè),x秒后pq∥bc,依題意有4x/20=(30-3x)/30.,即x/5=(10-x)/10.,化簡(jiǎn)得2x=10-x.解得x=10/3秒,2,當(dāng)s△bcq/s△abc=1/3時(shí),cq=1/3ac=10,,此時(shí)q由c出發(fā)運(yùn)動(dòng)10/3秒,pq∥bc,△apq∽△abc,s△apq/s△abc=(aq/ac)?=(2/3)?=4/9.
最新回答 更多>
相關(guān)問答
- 16C共享充電腫么使用?
- DNF遠(yuǎn)古1套有必要做嗎,本人55魔神,50CC+10怒靈套,其他都是任務(wù)給的。
- DNF現(xiàn)在50CC的短劍什么屬性 加什么技能和特別效果
- 一個(gè)棱長(zhǎng)20cm的正方體玻璃缸,里頭裝滿水,現(xiàn)在將水倒入一個(gè)長(zhǎng)20CM,寬16CM,深28Cm的空
- 請(qǐng)問時(shí)鐘芯片DS12887和DS12C887+有什么不同?
- 蠟燭每分鐘燃燒的長(zhǎng)度肯定,一根新蠟燭燃燒5分鐘后剩余長(zhǎng)度為15cm,繼續(xù)燃燒15分鐘后剩余長(zhǎng)度為5cm
- LM668怎么把時(shí)間設(shè)定在屏上?
- 蠟燭每分鐘燃燒的長(zhǎng)度肯定,一根新蠟燭燃燒5分鐘后剩余長(zhǎng)度為15cm,繼續(xù)燃燒15分鐘后剩余長(zhǎng)度為5cm
- 廣西一狂戰(zhàn)裝45到50CC大概賣多少?
- 已知:△DEF全等于△MNP,且EF=NP,∠F=∠P,∠D=48°,∠E=52°,MN=12cm,求∠P的度數(shù)及DE的長(zhǎng)。
- 把一個(gè)棱長(zhǎng)為8cm的正方體鍛造成一個(gè)長(zhǎng)方體長(zhǎng)方體長(zhǎng)是16cm,高是4cm寬是多少cm?長(zhǎng)方體的表面積是?
- 如圖,是從一塊邊長(zhǎng)為50cm的正方形材料截成的墊片,現(xiàn)測(cè)得FG=9cm,求墊片周長(zhǎng)。黑色部分為截出的墊片
- 為何我用CorelDraw12CHS復(fù)制圖片會(huì)出現(xiàn)文件復(fù)制錯(cuò)誤。臨時(shí)驅(qū)動(dòng)器或輸出驅(qū)動(dòng)器可能已滿
